線形代数 - Fight4354

この 2 日間の学習プロセスは、線形代数に対する理解を徐々に明確にしました。この投稿では、いくつかの重要な新しい内容をまとめます。

行列や特異値に直面したとき、次のような認識を持つべきです：
✅ 行列は空間の操作器です
✅ 特異値分解は行列の本質を分解します：回転 → 引き伸ばし → 回転
✅ 特異値の大きさの順序は、行列がどの方向に本当に力を持っているか、どの方向が無駄であるかを教えてくれます

1、直交行列#

直交行列（Orthogonal Matrix）の核心定義

ある $n \times n$ 実行列 $Q$ が次の条件を満たすとき、

$Q^{\mathsf T}\,Q \;=\; Q\,Q^{\mathsf T}\;=\;I_n$

$Q$ を直交行列と呼びます。
ここで $Q^{\mathsf T}$ は転置、 $I_n$ は $n$ 次単位行列です。

逆は転置です

Q^{-1}=Q^{\mathsf T}

計算が簡単で、数値的に安定しています。
直交行列は「内積を保持する」実行列です—— それは座標系を回転または反転させますが、決して引き伸ばしたり歪めたりしません。

2、尖括弧#

ここで

\langle q_i,\;q_j\rangle

は「内積 (inner product)」の記号です。最も一般的な状況 —— 実数ベクトル空間 $\mathbb R^n$ —— は、私たちが馴染みのある点積（dot product）と同等です：

\langle q_i,\;q_j\rangle \;=\; q_i^{\mathsf T}\,q_j \;=\; \sum_{k=1}^n (q_i)_k\,(q_j)_k.

3、行列の位置交換#

1. 左側の $Q$ を消去します

$S$ の左側にあるのは $Q$ です
それの逆 $Q^{-1}$ を左から掛けます：

Q^{-1}\,A \;=\; \cancel{Q^{-1}Q}\,S\,Q^{\mathsf T} \quad\Longrightarrow\quad Q^{-1}A \;=\; S\,Q^{\mathsf T}

注意：

左から掛ける際は必ず左右を一致させる必要があります；

$Q^{-1}$ を右側に掛けようとしないでください（それは積の順序を乱します）。

2. 右側の $Q^{\mathsf T}$ を消去します

$S$ の右側にあるのは $Q^{\mathsf T}$ です
それの逆 $(Q^{\mathsf T})^{-1}$ を右から掛けます：

Q^{-1}A(Q^{\mathsf T})^{-1} \;=\; S\cancel{Q^{\mathsf T}(Q^{\mathsf T})^{-1}} \quad\Longrightarrow\quad S = Q^{-1}A(Q^{\mathsf T})^{-1}

もし $Q$ が直交行列であれば、 $Q^{-1}=Q^{\mathsf T}$ となり、したがって

S \;=\; Q^{\mathsf T}\,A\,Q.

なぜ順序を逆にできないのか？

一度でも間違った側で掛けると、記号が別の位置に「挿入」されます：
$AQ^{-1} \neq Q^{-1}A$ 。
等号の両辺では必ず 対称的に 同じ操作を行わなければ、等式は成り立ちません。
これは本質的に関数の合成順序や座標変換の順序と同じです：どの変換を先に行うか、どの変換を後に行うかは、積の対応する位置に書かれ、決して自由に交換してはいけません。

4、相似対角化行列#

相似対角化行列（一般に「対角化可能行列」と呼ばれる）は次のように定義されます：

ある可逆行列 $P$ が存在して、次のように成り立つとき、

$P^{-1}AP = D,$

ここで $D$ は対角行列です。
このとき、 $A$ は相似変換によって対角化可能である、または略して $A$ は対角化可能であると言います。

対角化の「機械的プロセス」

固有値を求める： $\det(A-\lambda I)=0$ を解きます。
固有ベクトルを求める：各 $\lambda$ に対して、 $(A-\lambda I)x=0$ を解きます。
$P$ を組み立てる： $n$ 個の互いに独立な固有ベクトルを列として並べて行列 $P$ を作ります。
$D$ を得る：対応する固有値を対角線に埋め込みます： $D=\operatorname{diag}(\lambda_1,\dots,\lambda_n)$ 。
これにより $A = P D P^{-1}$ が得られます。

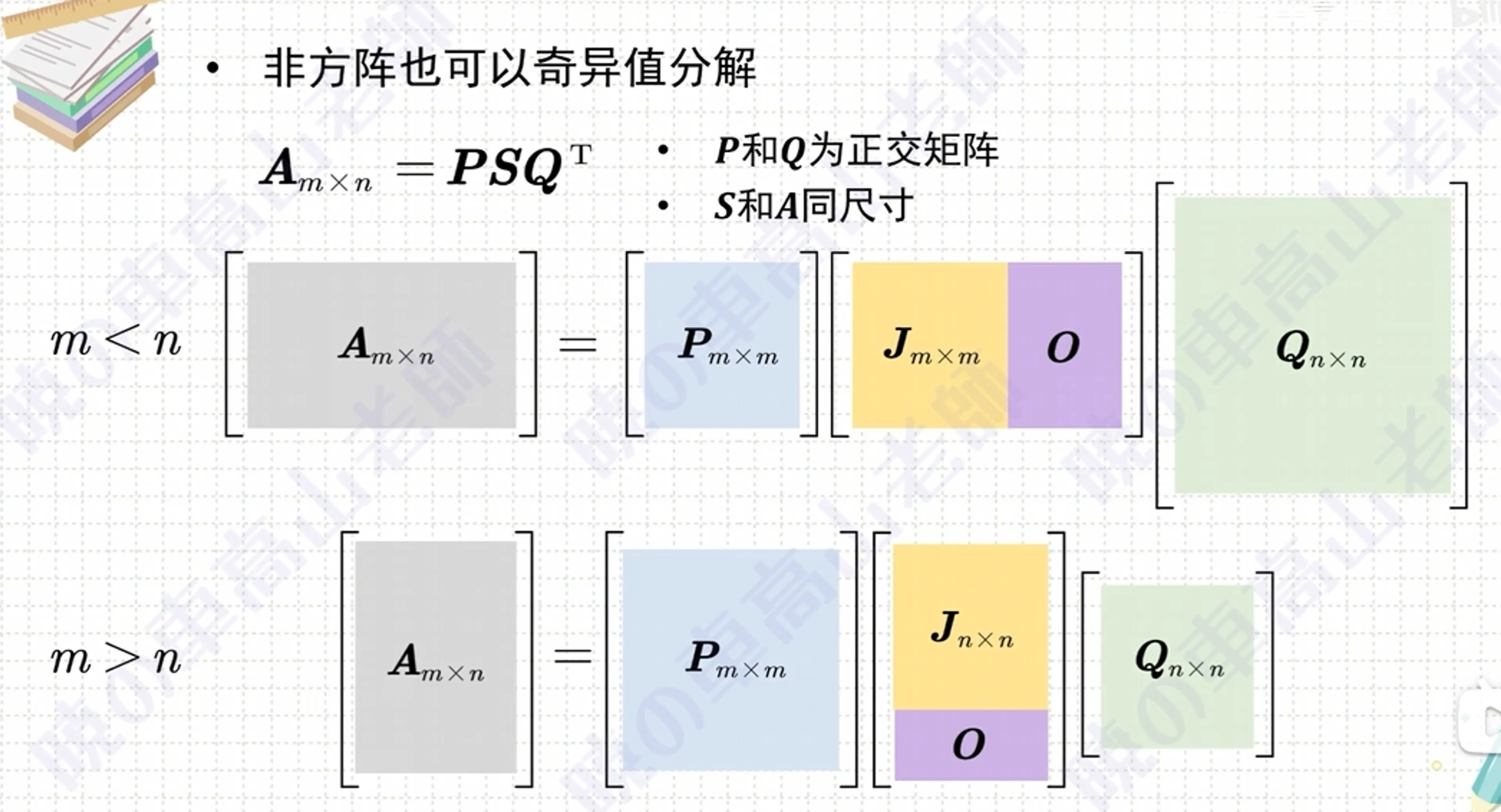
5、特異値分解#

A \;=\; Q\,S\,Q^{\mathsf T} \quad\Longleftrightarrow\quad S \;=\; Q^{\mathsf T} A Q

記号	意味
$A$	与えられた実対称行列（ $A^{\mathsf T}=A$ ）
$Q$	直交行列： $Q^{\mathsf T}Q=I$ 、列ベクトルは互いに直交し、単位長さを持つ
$S$	対角行列： $S=\operatorname{diag}(\lambda_1,\dots,\lambda_n)$

書き方 $A=Q S Q^{\mathsf T}$ は 直交相似対角化 と呼ばれ、幾何学的には「座標系を回転（または鏡像）→ A は独立の伸縮だけが残る」となります。

1. なぜ「実対称行列は必ず直交対角化できる」のか？

スペクトル定理：

任意の実対称行列 $A$ に対して、直交行列 $Q$ が存在し、 $Q^{\mathsf T} A Q$ は対角行列であり、対角成分は $A$ の固有値です。

実固有値：対称性が固有値が全て実数であることを保証します。
直交固有ベクトル：もし $\lambda_i \ne \lambda_j$ であれば、対応する固有ベクトルは必ず直交します。
重根も直交基を取ることができる：同じ固有値が複数のベクトルに対応する場合、それらが張る部分空間内で Gram–Schmidt を行うことで直交化できます。

文字のステップを逐条解析

ステップ	説明
1. $A$ の全ての固有値と固有ベクトルを求める	$\det(A-\lambda I)=0$ を計算して全ての $\lambda_i$ を得る；各 $\lambda_i$ に対して $(A-\lambda_i I)v=0$ を解いて固有ベクトルを求める。
2. 固有値を一定の順序で対角線に並べることで対角行列 $S$ を得る	例えば、昇順に $S=\operatorname{diag}(\lambda_1,\dots,\lambda_n)$ とします。順序は重要ではなく、後で列ベクトルの順序と一致すれば良いです。
3. 異なる固有値に対応する固有ベクトルは互いに直交する；重根の固有ベクトルは Gram-Schmidt で直交化し、単位化する	- $\lambda_i\neq\lambda_j$ の場合、対応するベクトルは自然に直交しており、何もする必要はありません。

$\lambda$ が重複している場合（幾何的重複度 >1）、適当に線形独立なベクトルのグループを取って、再度 Gram-Schmidt を行い、互いに直交し、各自の長さを 1 にします。 |
| 4. 固有値の対角線上の順序に従って改造された固有ベクトルを横に並べることで、直交行列 $Q$ を得る | 対角線の固有値の順序に従って改造された固有ベクトルを列として並べて $Q=[q_1\ \cdots\ q_n]$ を得ます。この時 $Q^{\mathsf T}Q=I$ となり、 $A = Q S Q^{\mathsf T}$ も成り立ちます。 |

具体的な $2 \times 2$ の小例

設定

A=\begin{bmatrix} 4 & 1\\ 1 & 4 \end{bmatrix}

① 固有値を求める

\det(A-\lambda I)=(4-\lambda)^2-1=0 \Longrightarrow \lambda_1=5,\; \lambda_2=3

② 固有ベクトルを求める

$\lambda_1=5$ ： $(A-5I)v=0 \ \Rightarrow\ v_1=\begin{bmatrix}1\\1\end{bmatrix}$
$\lambda_2=3$ ： $(A-3I)v=0 \ \Rightarrow\ v_2=\begin{bmatrix}1\\-1\end{bmatrix}$

③ 単位化

q_1=\frac{1}{\sqrt2}\begin{bmatrix}1\\1\end{bmatrix},\quad q_2=\frac{1}{\sqrt2}\begin{bmatrix}1\\-1\end{bmatrix}

④ 組み立てて検証

Q=\frac1{\sqrt2}\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix},\quad S=\begin{bmatrix}5&0\\0&3\end{bmatrix},\quad Q^{\mathsf T} A Q = S.

6、行列式（det・）#

行列式（determinant）は、正方行列 $A$ をスカラー $\det A$ にマッピングする演算です。
このスカラーは、行列の最も核心的な幾何学的および代数的情報を統合します：体積の伸縮因子、可逆性、固有値の積など。

公式

階数	公式
$1\times1$	$\det[a]=a$
$2\times2$	$\displaystyle\det\!\begin{bmatrix}a&b\\c&d\end{bmatrix}=ad-bc$
$3\times3$	「サリュス法」または第一行に沿って展開：
$\displaystyle \det\!\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}=a(ei-fh)-b(di-fg)+c(dh-eg)$
核心的性質（どの定義も満たす必要があります）

性質	説明
乗法性	$\det(AB)=\det A\cdot\det B$
可逆判定	$\det A\neq0 \iff A$ は可逆
行列の線形性	各行（列）は要素に関して線形
交替性	二行（列）を交換すると行列式の符号が変わる
対角線の積	上 / 下三角行列： $\det A=\prod_{i}a_{ii}$
固有値の積	$\det A=\lambda_1\lambda_2\cdots\lambda_n$ （重複を含む）

3×3 の手計算例

設定

A=\begin{bmatrix} 2 & 1 & 3\\ 0 & 4 & -1\\ 5 & 2 & 0 \end{bmatrix}

第一行に沿って展開します：

\begin{aligned} \det A &= 2\;\det\!\begin{bmatrix}4&-1\\2&0\end{bmatrix} \;-\;1\;\det\!\begin{bmatrix}0&-1\\5&0\end{bmatrix} \;+\;3\;\det\!\begin{bmatrix}0&4\\5&2\end{bmatrix} \\[4pt] &= 2\,(4\cdot0-(-1)\cdot2) -1\,(0\cdot0-(-1)\cdot5) +3\,(0\cdot2-4\cdot5) \\[4pt] &= 2\,(2) -1\,(5) +3\,(-20) \\[4pt] &= 4 - 5 - 60 = -61. \end{aligned}

一言でまとめる

「行列式を取る」とは： $n\times n$ の正方行列を一連の交替的かつ線形の規則に従って単一の数字に圧縮することであり、この数字は行列の体積の伸縮、方向、可逆性、固有値の積などの重要な情報を同時にエンコードしています。

7、行列のランク#

行列の「ランク」とは一体何でしょうか？

等価な視点	直感的な説明
線形独立	行（または列）の中からどれだけの互いに線形独立なベクトルを選べるかがランクです。
空間の次元	列ベクトルが張る部分空間（列空間）の次元 = 行ベクトルが張る部分空間（行空間）の次元 = ランク。
満ランクの行列式	行列の中で最大の非ゼロ行列式の階数 = ランク。
特異値	SVD $A=U\Sigma V^{\!}$ において、非ゼロ特異値*の個数 = ランク。

線形独立
以下に 3 × 3 の小さな行列を使って、ランクが「どれだけの線形独立な列（または行）ベクトルを選べるか」ということを明確に示します。

| 行列 $A$ | 列ベクトルを $\bigl(v_1\,|\,v_2\,|\,v_3\bigr)$ として書く | 線形関係 | ランク |
|------------|-----------------------------------------------|-----------|--------|
| $\displaystyle\begin{bmatrix}1&2&3\\2&4&6\\3&6&9\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\2\\3\end{bmatrix}$
$v_2=\begin{bmatrix}2\\4\\6\end{bmatrix}=2v_1$
$v_3=\begin{bmatrix}3\\6\\9\end{bmatrix}=3v_1$ | 三列全てが同一直線上にある ——独立なベクトルは 1 本だけ | 1 |
| $\displaystyle\begin{bmatrix}1&0&1\\0&1&1\\1&1&2\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\0\\1\end{bmatrix}$
$v_2=\begin{bmatrix}0\\1\\1\end{bmatrix}$
$v_3=v_1+v_2$ | $v_1, v_2$ は共線でない ⇒ 2 次元平面； $v_3$ はこの平面上にある | 2 |
| $\displaystyle\begin{bmatrix}1&0&1\\0&1&1\\1&1&0\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\0\\1\end{bmatrix}$
$v_2=\begin{bmatrix}0\\1\\1\end{bmatrix}$
$v_3=\begin{bmatrix}1\\1\\0\end{bmatrix}$ | 任意の二列は第三列を線形に表現できない ⇒ 三列が全て $\mathbb R^{3}$ を張る | 3 |

「無関係」を判断する方法は？

手計算 列を行列にまとめて、消去を行う → 非ゼロ行の数がランクです。
概念もし定数 $c_1,c_2,c_3$ が存在して $c_1v_1+c_2v_2+c_3v_3=0$ かつ全てが 0 でない場合、ベクトルは関連しています；そうでなければ無関係です。
- ケース 1：$2v_1-v_2=0$ → 関連しています
- ケース 2：$v_3=v_1+v_2$ のみが関連しており、$v_1,v_2$ は無関係です
- ケース 3：どの非自明な組み合わせも ≠ 0 → 三つのベクトルは全て独立です

一言で言うと：ランク = この行列が本当に「保持できる」独立情報の数（次元）。

8、低ランク近似#

なぜ SVD の切り捨て（低ランク近似）で k (m+n)+k 個の数だけを保存すれば良いのか？

元の行列

A\in\mathbb R^{m\times n}

をランク $k$ に切り捨てて次のように書くと

A_k \;=\; U_k \,\Sigma_k \, V_k^{\mathsf T},

ブロック	形状	保存する必要のあるスカラーの数	説明
$U_k$	$m\times k$	$m \times k$	左特異ベクトル：最初の $k$ 列のみを取ります
$V_k$	$n\times k$	$n \times k$	右特異ベクトル：同様
$\Sigma_k$	$k\times k$ 対角	$k$	対角線上の $k$ 個の特異値のみを保持します

これら三つを合計すると

\underbrace{m k}_{U_k} \;+\; \underbrace{n k}_{V_k} \;+\; \underbrace{k}_{\Sigma_k} \;=\; k\,(m+n)+k.

$U_k$ と $V_k$ ：それぞれ $k$ 列を持ち、各列は行数の長さのベクトルを保存します
$\Rightarrow mk + nk$ 個の数。
$\Sigma_k$ ：対角行列で、 $k$ 個の対角要素のみが必要です —— $k^2$ ではありません。

したがって、ランク - $k$ の SVD 近似を用いて元の $m\times n$ の保存量を置き換えると、パラメータ量は $mn$ から $k(m+n)+k$ に縮小されます。
もし $k \ll \min(m,n)$ であれば、節約されるスペースは非常に大きくなります。

ランクの低下 = 情報の次元の低下、低ランクの保存 = パラメータ量 / メモリの同時低下

9、ノルム#

「二本の縦線」 $|,\cdot,|$ は線形代数において ノルム（norm） を表します。

ベクトル $v\in\mathbb R^m$ に対して、最も一般的なのは 二ノルム（Euclidean norm）： $\|v\|=\sqrt{v^{\mathsf T}v}=\sqrt{\sum_{i=1}^{m}v_i^{2}},\qquad \|v\|^{2}=v^{\mathsf T}v.$
図中の $\|Xw-y\|^{2}$ は、ベクトル $Xw-y$ の各成分を平方して合計することを意味します。
行列 $A$ に対して $\|A\|$ と書かれる場合、通常は フロベニウスノルム（Frobenius norm）を意味します： $\|A\|_F=\sqrt{\sum_{i,j}A_{ij}^{2}}$ 。ただし、この図ではベクトルに関するものです。

これに対して、単一の縦線 $|\,\cdot\,|$ は通常、絶対値（スカラー）または行列式 $|A|$ を表します。したがって、二本の縦線はベクトル / 行列の「長さ」の記号であり、単一の縦線はスカラーの大きさまたは行列式の記号であり —— 対象と意味が異なります。

ベクトルの一般的なユークリッド距離 -- 2 ノルム（L2 ノルム）#

import torch

b = torch.tensor([3.0, 4.0])
print(b.norm())  # 出力 5.0

.norm() は PyTorch テンソル（torch.Tensor） のメソッドです。

行列の一般的なフロベニウスノルム#

行列にも「長さ」があり、一般的には フロベニウスノルム が使用されます

名称	記号	公式（対 $A\in\mathbb R^{m\times n}$ ）	ベクトルとの類似
フロベニウスノルム	$\displaystyle\|A\|_F$	$\displaystyle\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}A_{ij}^{2}}$	ベクトルの 2 - ノルム $\|v\|=\sqrt {\sum v_i^2}$ のように

1. なぜ「行列の内積」としても書けるのか

行列空間で一般的に使用される内積は

\langle A,B\rangle := \operatorname{tr}\!\bigl(A^{\mathsf T}B\bigr),

ここで $\operatorname{tr}(\cdot)$ はトレース演算（対角線要素の和）です。
$A$ 自身に対してこの内積を取ると、

\|A\|_F^{2} \;=\;\langle A,A\rangle \;=\;\operatorname{tr}\!\bigl(A^{\mathsf T}A\bigr).

したがって：

$\boxed{\;\|A\|_F^{2}= \operatorname{tr}(A^{\mathsf T}A)\;}$

これは行列版の $\|v\|^{2}=v^{\mathsf T}v$ であり —— ただベクトルの内積を「トレース内積」に置き換えたものです。
フロベニウスノルムは実際に全ての特異値の平方和の平方根に等しい、すなわち：

\| A \|_F = \sqrt{\sum_i \sigma_i^2}

ここで：

$| A |_F$ は行列 $A$ のフロベニウスノルムです
$\sigma_i$ は $A$ の特異値です

フロベニウスノルムは実際に全ての特異値の平方和の平方根に等しい
展開して説明します：

フロベニウスノルムは次のように定義されます：

\| A \|_F = \sqrt{ \sum_{i,j} |a_{ij}|^2 }

しかし特異値分解（SVD）は次のように教えてくれます：

A = U \Sigma V^T

ここで $\Sigma$ は対角行列で、主対角線上には特異値 $\sigma_1, \sigma_2, \dots$ が存在します。

フロベニウスノルムは変換を変えない（単位直交変換はノルムを変えない）ため、直接計算できます：

\| A \|_F^2 = \sum_{i,j} |a_{ij}|^2 = \sum_i \sigma_i^2

したがって最終的に：

\| A \|_F = \sqrt{ \sum_i \sigma_i^2 }

注意すべき点

注意：
✅ 単一の特異値の平方根でもなく、最大の特異値でもありません
✅ 全ての特異値を平方してから合計して平方根を取ったものです

スペクトルノルムは「最も拡大する方向」を見ますが、フロベニウスは全てのエネルギーを累積します。

行列のスペクトルノルム#

✅ スペクトルノルムの定義

行列 $A$ のスペクトルノルム（spectral norm）は次のように定義されます：

\| A \|_2 = \max_{\|x\|_2 = 1} \| A x \|_2

直訳すると、行列 $A$ が単位ベクトルをどれだけ引き伸ばすかの最大値です。
特異値は元々行列の引き伸ばし変換を表すものです。

これは $A$ の最大特異値に等しいです：

\| A \|_2 = \sigma_{\max}(A)

別の視点：スペクトルノルム ≈ 単位ベクトルを行列に入れたときに引き伸ばされる最大の長さ
✅ フロベニウスノルムとの関係

フロベニウスノルム → 全体のエネルギー（行列要素の平方和）を見る
スペクトルノルム → 単一の方向での最大の引き伸ばし量を見る

言い換えれば：

フロベニウスは行列の「体積」の総量を見ます
スペクトルノルムは「最も極端な」単一方向の拡大率を見ます

✅ 例：なぜそれが重要なのか？

神経ネットワークの線形層 $W$ を想像してください：

もし $\| W \|_2$ が非常に大きいと、入力のわずかな摂動が拡大され、
ネットワークは過剰適合しやすく、ノイズに敏感になります。
もし $\| W \|_2$ が適度であれば、ネットワークの出力の変化は入力の摂動に対して安定し、
一般化能力が向上します。

したがって、現代の手法（例えばスペクトル正規化）は、
訓練中に $W$ のスペクトルノルムをある範囲に抑えることを直接行います。

⚠ 欠点を率直に述べる

スペクトルノルムは強力ですが：

単一の最大方向にのみ注目し、他の方向の拡大を無視します；
フロベニウスノルムより計算が複雑です（特異値分解が必要で、単純な要素の平方和ではありません）。

概要の比較

	ユークリッドノルム (2-norm, ‖v‖)	フロベニウスノルム (‖A‖_F)
対象	ベクトル $v\in\mathbb R^{n}$	行列 $A\in\mathbb R^{m\times n}$
定義	$\displaystyle\\|v\\|=\sqrt{\sum_{i=1}^{n}v_i^{2}}$	$\displaystyle\\|A\\|_F=\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}A_{ij}^{2}}$
等価な表現	$\\|v\\|^{2}=v^{\mathsf T}v$	$\\|A\\|_F^{2}=\operatorname{tr}(A^{\mathsf T}A)=\sum_{k}\sigma_k^{2}$
幾何学的意味	ベクトルの $n$ 次元ユークリッド空間における長さ	行列要素を「長いベクトル」として見たときの長さ
単位 / 尺度	座標軸と同じ尺度を持つ	同上；行列の形状に依存しない
一般的な用途	誤差測定、正則化 $L^2$ 、距離	重み減衰、行列近似誤差、カーネル法
スペクトルノルムとの関係	$\\|v\\|=\sigma_{\max }(v)$ (単一の特異値のみ)	$\\|A\\|_F\ge \\|A\\|_2=\sigma_{\max }(A)$ ；ランクが 1 の場合は等しい

1. 同じ考え方、異なる次元

ユークリッドノルムは ベクトル自身と自分自身の内積を取った後に平方根を取る。
フロベニウスノルムは行列の各要素を長いベクトルとして見て、同じことを行います；行列の言葉で書くと

$\|A\|_F=\sqrt{\operatorname{tr}(A^{\mathsf T}A)}.$

これは「転置 → 乗算 → トレースを取る」ことです。

2. どのような場合にどちらを使用するか？

シーン	推奨ノルム	理由
予測誤差、勾配降下	ユークリッド (ベクトル残差)	残差は自然に列ベクトルです
ネットワークの重み正則化 (Dense / Conv)	フロベニウス	パラメータの形状に関心がなく、全体の大きさのみを気にします
行列近似の質を比較 (SVD, PCA)	フロベニウス	特異値の平方和に簡単に対応します
安定性 / リプシッツ境界	スペクトルノルム ( $\\|A\\|_2$ )	拡大率に関心があり、全体のエネルギーには関心がありません

3. 直感的な違い

ユークリッド：量 単一方向 の長さ；
フロベニウス：量 各要素のエネルギー の総和であり、したがって行列にとっては、どの列や行も特別ではなく、全ての要素が平等に扱われます。

一言で記憶する：

ユークリッドノルム：ベクトルの「定規」。
フロベニウスノルム：行列を「平らに」した後、同じ定規でその全体の大きさを測る。

10、行列の積の転置#

行列代数において、二つ（またはそれ以上）の行列の積の転置には固定の「反転順序」ルールがあります：

(AB)^{\mathsf T}=B^{\mathsf T}\,A^{\mathsf T}.

つまり 各行列を転置した後、乗法の順序を逆にします。
この性質は、任意の次元に一致する実（または複素）行列に対して成り立ち、再帰的に拡張できます：

(ABC)^{\mathsf T}=C^{\mathsf T}\,B^{\mathsf T}\,A^{\mathsf T},\qquad (\,A_1A_2\cdots A_k)^{\mathsf T}=A_k^{\mathsf T}\cdots A_2^{\mathsf T}A_1^{\mathsf T}.

xLog 編集 Markdown 文書の注意事項

すべての数学表現が $$ … $$ を使用していることを確認してください
もし $n \times n$ のような単一の $ があれば、n × n または $$n\\times n$$ に変更します

参考動画：

こちらをクリックして B ステーションの動画を見る