Fight4354

这两天的学习过程对线性代数的认知逐渐清晰，我以此贴，把一些关键新内容汇总于此。

当面对矩阵、奇异值时，应该建立如下认知：
✅ 矩阵是空间操作器
✅ 奇异值分解帮你分解矩阵的精髓：旋转 → 拉伸 → 旋转
✅ 奇异值的大小排序，告诉你：矩阵在哪些方向上真正有力量，哪些方向是废

1、正交矩阵#

正交矩阵（Orthogonal Matrix）的核心定义

一个 $n \times n$ 实矩阵 $Q$ 如果满足

Copy$$Q^{\mathsf T}\,Q \;=\; Q\,Q^{\mathsf T}\;=\;I_n$$

则称 $Q$ 为正交矩阵。
这里 $Q^{\mathsf T}$ 是转置，$I_n$ 是 $n$ 阶单位矩阵。

逆即转置

计算上省事，数值稳定。
正交矩阵就是 “保持内积” 的实矩阵—— 它把坐标系旋转或翻转，但绝不拉伸或扭曲。

2、尖括号#

在这里

就是 “内积 (inner product)” 的符号。最常见的情形 —— 实数向量空间 $\mathbb R^n$—— 它等同于我们熟悉的点积（dot product）：

3、矩阵交换位置#

1. 消掉左边的 $Q$

• 贴在 $S$左边的是 $Q$

• 用它的逆 $Q^{-1}$左乘双方：

注意：

• 必须左右一致地左乘；

• 不要尝试把 $Q^{-1}$乘到右边去（那会打乱乘积顺序）。

2. 消掉右边的 $Q^{\mathsf T}$

• 贴在 $S$ 右边的是 $Q^{\mathsf T}$

• 用它的逆 $(Q^{\mathsf T})^{-1}$右乘双方：

若 $Q$ 是正交矩阵，$Q^{-1}=Q^{\mathsf T}$，于是

为什么顺序不能颠倒？

• 一旦乘错侧，符号会 “插” 到别的位置：
  $AQ^{-1} \neq Q^{-1}A$。

• 在等号两边必须 对称地 进行相同操作，等式才仍然成立。

• 这本质上与函数复合顺序或坐标变换顺序相同：先做哪个变换、后做哪个变换都写在乘积的对应位置，绝不能随意交换。

4、相似对角化矩阵#

相似对角化矩阵（常说 “可对角化矩阵”）指的是：

存在一个可逆矩阵 $P$，使得

Copy$$P^{-1}AP = D,$$

其中 $D$ 是对角矩阵。
此时说 $A$ 能通过相似变换被对角化，或简称 $A$ 可对角化。

对角化的 “机械流程”

1. 求特征值：解 $\det(A-\lambda I)=0$。

2. 求特征向量：对每个 $\lambda$，解 $(A-\lambda I)x=0$。

3. 组装 $P$：把 $n$ 个互不相关的特征向量按列排成矩阵 $P$。

4. 得到 $D$：把对应特征值填进对角线：$D=\operatorname{diag}(\lambda_1,\dots,\lambda_n)$。
   就有 $A = P D P^{-1}$。

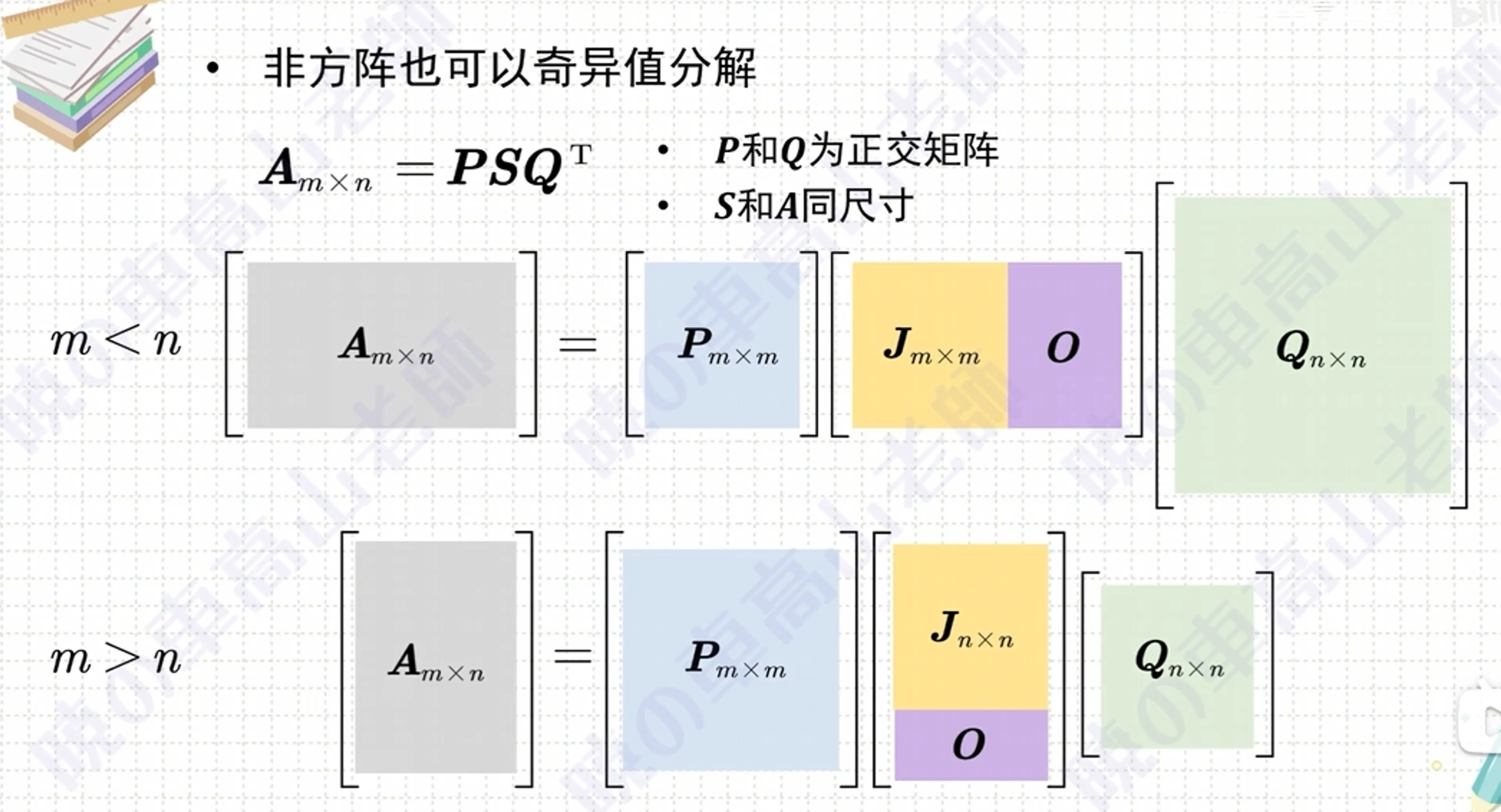
5、奇异值分解#

写法 $A=Q S Q^{\mathsf T}$ 称为 正交相似对角化；几何上就是 “旋转（或镜像）坐标系 → A 只剩独立的伸缩”。

1. 为什么 “实对称矩阵一定能正交对角化”？

光谱定理：

对任何实对称矩阵 $A$，存在正交矩阵 $Q$ 使得 $Q^{\mathsf T} A Q$ 是对角的，且对角元就是 $A$ 的特征值。

• 实特征值：对称保证特征值全是实数。
• 正交特征向量：若 $\lambda_i \ne \lambda_j$，对应特征向量必正交。
• 重根也能取正交基：同一特征值可能对应多个向量，这时在它们张成的子空间里再做 Gram–Schmidt 即可。

2. 文字步骤逐条解析

3. 一个 $2 \times 2$ 具体小例子

设

① 求特征值

② 求特征向量

• $\lambda_1=5$：$(A-5I)v=0 \ \Rightarrow\ v_1=\begin{bmatrix}1\\1\end{bmatrix}$
• $\lambda_2=3$：$(A-3I)v=0 \ \Rightarrow\ v_2=\begin{bmatrix}1\\-1\end{bmatrix}$

③ 归一化

④ 组装并验证

6、取行列式（det・）#

行列式（determinant）是把一个方阵 $A$ 映射成一个标量 $\det A$ 的运算。
这个标量综合了矩阵最核心的几何与代数信息：体积伸缩因子、可逆性、特征值乘积等。

公式

3×3 手算示例

设

按第一行展开：

一句话总结

“取行列式” 就是：让一个 $n\times n$ 方阵通过一套交替、线性的规则坍缩成单一数字，这个数字同时编码了矩阵的体积伸缩、方向、可逆性和特征值乘积等关键信息。

7、矩阵的秩#

矩阵的 “秩” 到底是什么？

线性独立
下面用 3 × 3 的小矩阵举三个对比案例，让「秩 = 能挑出几根线性无关的列（或行）向量」这句话一目了然。

| 矩阵 $A$ | 列向量写成 $\bigl(v_1\,|\,v_2\,|\,v_3\bigr)$ | 线性关系 | 秩 |
|------------|-----------------------------------------------|-----------|--------|
| $\displaystyle\begin{bmatrix}1&2&3\\2&4&6\\3&6&9\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\2\\3\end{bmatrix}$
$v_2=\begin{bmatrix}2\\4\\6\end{bmatrix}=2v_1$
$v_3=\begin{bmatrix}3\\6\\9\end{bmatrix}=3v_1$ | 三列全在同一直线上 ——只有 1 根独立向量 | 1 |
| $\displaystyle\begin{bmatrix}1&0&1\\0&1&1\\1&1&2\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\0\\1\end{bmatrix}$
$v_2=\begin{bmatrix}0\\1\\1\end{bmatrix}$
$v_3=v_1+v_2$ | $v_1, v_2$ 不共线 ⇒ 2 维平面；$v_3$ 落在这平面里 | 2 |
| $\displaystyle\begin{bmatrix}1&0&1\\0&1&1\\1&1&0\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\0\\1\end{bmatrix}$
$v_2=\begin{bmatrix}0\\1\\1\end{bmatrix}$
$v_3=\begin{bmatrix}1\\1\\0\end{bmatrix}$ | 任意两列都无法线性表达第三列 ⇒ 三列张成整个 $\mathbb R^{3}$ | 3 |

如何判断「无关」？

• 手算 把列拼成矩阵，对它做消元 → 非零行数就是秩。

• 概念 如果存在常数 $c_1,c_2,c_3$ 使 $c_1v_1+c_2v_2+c_3v_3=0$ 且不全为 0，向量就相关；否则无关。

  • 案例 1：$2v_1-v_2=0$ → 相关

  • 案例 2：只有 $v_3=v_1+v_2$ 相关，$v_1,v_2$ 无关

  • 案例 3：任何非平凡组合都 ≠ 0 → 三向量全独立

一句话：秩 = 这张矩阵真正 “存得下” 多少独立信息（维度）。

8、低秩近似#

为什么截断 SVD (低秩近似) 只要存 k (m+n)+k 个数？

把原矩阵

截断到秩 $k$ 后写成

把三块加起来就是

• $U_k$ 和 $V_k$：各有 $k$ 列，每列存一个长度为行数的向量
  $\Rightarrow mk + nk$ 个数。

• $\Sigma_k$：是对角矩阵，只需那 $k$ 个对角元素 —— 不是 $k^2$。

因此，用秩 -$k$ 的 SVD 近似替代原来的 $m\times n$ 储存量，参数量从 $mn$ 缩到 $k(m+n)+k$。
如果 $k \ll \min(m,n)$，省下的空间就非常可观。

秩降低 = 信息维度降低，低秩存储 = 参数量 / 内存同步降低

9、范数#

“两竖线” $|,\cdot,|$ 在线性代数里表示 范数（norm）。

• 对向量 $v\in\mathbb R^m$，最常用的是 二范数（Euclidean norm）：$\|v\|=\sqrt{v^{\mathsf T}v}=\sqrt{\sum_{i=1}^{m}v_i^{2}},\qquad \|v\|^{2}=v^{\mathsf T}v.$
  在图中 $\|Xw-y\|^{2}$ 就是把向量 $Xw-y$ 的每个分量平方后求和。

• 对矩阵 $A$ 若也写 $\|A\|$，常默认为 Frobenius 范数：$\|A\|_F=\sqrt{\sum_{i,j}A_{ij}^{2}}$。不过在这张图里涉及的都是向量。

与之对比，单竖线 $|\,\cdot\,|$ 通常表示绝对值（标量）或行列式 $|A|$。所以双竖线是向量／矩阵 “长度” 的符号，单竖线是标量大小或行列式的符号 —— 对象和含义都不同。

向量常用欧几里得距离 -- 2 范数（L2 范数）#

import torch

b = torch.tensor([3.0, 4.0])
print(b.norm())  # 输出 5.0

.norm() 是 PyTorch 张量（torch.Tensor） 的方法。

矩阵常用 Frobenius 范数#

矩阵也有 “长度”—— 常用的是 Frobenius 范数

1. 为什么也能写成 “矩阵点积”

在矩阵空间里常用的 内积 是

其中 $\operatorname{tr}(\cdot)$ 是迹运算（对角线元素之和）。
给 $A$ 自己做这个内积，就得到

所以：

  

Copy$$\boxed{\;\|A\|_F^{2}= \operatorname{tr}(A^{\mathsf T}A)\;}$$

这正是矩阵版本的 $\|v\|^{2}=v^{\mathsf T}v$—— 只是把向量点积换成了 “迹点积”。
Frobenius 范数确实等于所有奇异值平方和的平方根，也就是：

这里：

• $| A |_F$ 是矩阵 $A$ 的 Frobenius 范数

• $\sigma_i$ 是 $A$ 的奇异值

Frobenius 范数确实等于所有奇异值平方和的平方根
展开解释：

Frobenius 范数定义为：

但奇异值分解（SVD）告诉我们：

其中 $\Sigma$ 是对角矩阵，主对角线上就是奇异值 $\sigma_1, \sigma_2, \dots$。

因为 Frobenius 范数不变换（单位正交变换不改变范数），我们可以直接算：

所以最终：

小心误区

注意：
✅ 不是 单个奇异值平方根，也不是最大奇异值
✅ 是 所有奇异值平方后再相加取根号

谱范数看 “最能放大的一个方向”，Frobenius 则把所有能量都累加

矩阵的谱范数#

✅ 谱范数定义

矩阵 $A$ 的谱范数（spectral norm）定义为：

直白讲，就是 矩阵 $A$ 把单位向量拉伸到多长的最大值。
奇异值本来就是表示矩阵的拉伸变换的。

它等于 $A$ 的最大奇异值：

另一角度：谱范数 ≈ 把单位向量丢进矩阵后被拉伸的最大长度
✅ 它跟 Frobenius 范数的关系

• Frobenius 范数 → 看整体能量（矩阵元素平方和）

• 谱范数 → 看单个方向上最大拉伸量

换句话说：

• Frobenius 像是矩阵 “体积” 总量感

• 谱范数像是 “最极端” 的单一方向放大率

✅ 例子：为什么它重要？

想象一个神经网络的线性层 $W$：

• 如果 $\| W \|_2$ 非常大，输入的微小扰动会被放大，
  网络容易过拟合，对噪声敏感。

• 如果 $\| W \|_2$ 适度，网络输出变化对输入扰动就稳定，
  泛化能力更好。

所以现代方法（比如 spectral normalization）
会直接在训练中把 $W$ 的谱范数压制到一个范围内。

⚠ 直说缺点

谱范数很强，但：

• 只关注单一最大方向，忽略了其他方向的放大；

• 计算比 Frobenius 范数复杂（需要奇异值分解，而不是简单元素平方和）。

概要对比

1. 同一思路、不同维度

• 欧几里得范数是 向量自身与自己做点积后开方。

• Frobenius 范数把矩阵各元素看成一条长向量，再做同样的事；用矩阵语言写成

  Copy$$\|A\|_F=\sqrt{\operatorname{tr}(A^{\mathsf T}A)}.$$

  这就是 “转置 → 乘 → 取迹”。

2. 何时用哪个？

3. 直观区别

• 欧几里得：量 单个方向 的长度；

• Frobenius：量 每个元素能量 的总和，因此对矩阵来说，哪一列或哪一行并不特殊，所有元素一视同仁。

一句话记忆：

欧几里得 范数：向量 “标尺”。
Frobenius 范数：把矩阵 “铺平” 后用同一把标尺量它的整体大小。

10、矩阵相乘的转置#

在矩阵代数里，两个（或多个）矩阵相乘后的转置有一个固定的 “翻转顺序” 规则：

也就是说 先转置每个矩阵，再把乘法顺序倒过来。
这一条性质对任何维度匹配的实（或复）矩阵都成立，而且可以递归推广：

xLog 编辑 Markdown 文档注意内容

• 确认所有数学表达式都用 $$ … $$

• 如果有 $n \times n$ 之类单 $，改成 n × n 或 $$n\\times n$$

参考视频：

点这里看 B 站视频